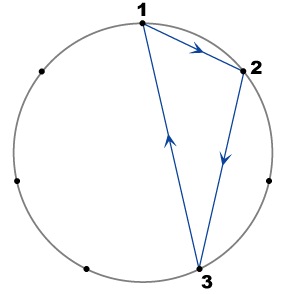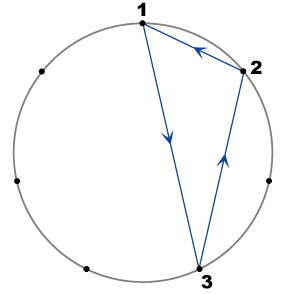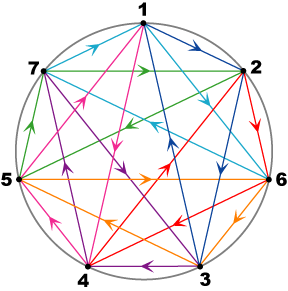
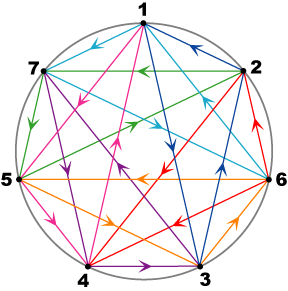
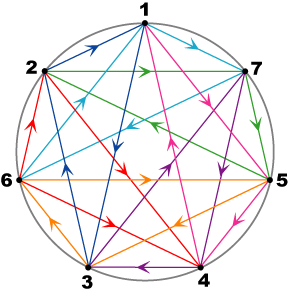
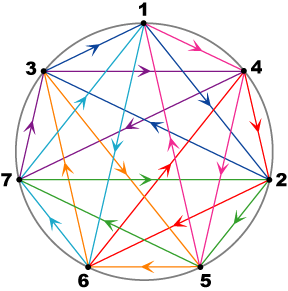
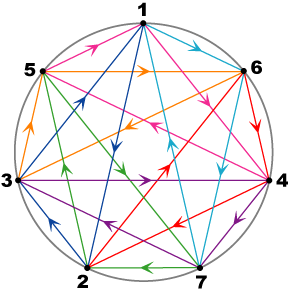
A Geometrical Representation of the Fano Plane and Octonionic Multiplication

The unit elements and triads of the octonions can be graphically represented in a way that illuminates a relation to projective geometry, and aids the analysis of symmetries, etc. The twisted octonions are also clearly distinguished, and counts of representations are facilitated.

Fano Plane

A projective plane is a set of "points", and "lines" containing the points, so as to satisfy the axioms: Note that interchanging "point" and "line" yields the same axioms (self-duality).

A simple system (known as the Fano plane) satisfying these axioms consists of 7 points grouped into overlapping triads (the "lines") such that each pair of distinct points determines a unique line (triad) - the very same criteria for arranging multiplicative closure in the triads of the octonion multiplication table. A useful geometric representation will now be constructed that embodies the axioms above, and facilitates the generation of octonionic multiplication tables.

Start with a circle having 7 equally spaced points on the circumference (i.e. at intervals of 2π/7), including a point at the top, labeled "1" for easy reference. Lines (triads) will be represented by triangles with vertices on the circumferential points, such that the entire set of triangles can be obtained from any one by successive rotations of 2π/7. Since each pair of units belongs to exactly one triad, any triad's triangle cannot be isoceles (otherwise the same pair of points would be included in two different rotational positions of the triangle, corresponding to 2 distinct lines). Trying the different possible triangles thus leads to a shape unique up to mirror image, with one side joining adjacent points and no 2 sides equal, as in Figures 1a and 1b (showing the 2 possible triangles for point "1" and its nearest neighbor going clockwise).

Figure 1a.
Figure 1b.
Drawing all 7 triangles and comparing their properties to the axioms shows that the system is indeed a projective plane.

Octonion Multiplication Tables

To relate the diagrams to representations of octonionic multiplication, label the remaining points with any permutation of {2, 3, 4, 5, 6} so that the circumferential points represent the imaginary units. To make these triangles embody the quaternionic multiplication table of the triad, a direction will be given, as indicated by arrowheads, so that Figure 1a gives Figures 2a and 2b below (with similar, mirror-image evolution for Fig. 1b).

Figure 2a.
Figure 2b.
The direction of the triangle will indicate the handedness of the triad, so that Figure 2a represents:
while Figure 2b represents:
Proceeding with the development of Figure 2a via rotations of the triangle through successive increments of 2π/7, and (arbitrarily) assigning further imaginary units to the new vertices generated gives Figure 3 (with different colors for different triads). Following each triangle around shows that the diagram represents the octonion representation with triads:
(e1, e2, e3)
(e2, e6, e4)
(e6, e3, e5)
(e3, e4, e7)
(e4, e5, e1)
(e5, e7, e2)
(e7, e1, e6)
 ⇔
(cyclic permutation of triads
til lowest index first) 		(e1, e2, e3)
(e2, e6, e4)
(e3, e5, e6)
(e3, e4, e7)
(e1, e4, e5)
(e2, e5, e7)
(e1, e6, e7)
 ⇔
(lexically reorder triad list) 		(e1, e2, e3)
(e1, e4, e5)
(e1, e6, e7)
(e2, e6, e4)
(e2, e5, e7)
(e3, e4, e7)
(e3, e5, e6)
recognized from the octonion representation table as signmask 08 of line 0 (the XOR quaternionic grouping).
Figure 3
To count how many distinct octonion multiplication tables are generated by all variants of this construction method, permute the labels on the vertices, and factor out the degeneracies (i.e. the different diagrams that yield the same octonion representation). The choice made earlier to label the topmost vertex as "1" (corresponding to imaginary unit e1) is to eliminate a trivial 7-fold degeneracy i.e. rotating the entire diagram by 2Nπ/7 and thereby moving vertex "1" to one of the other 6 positions produces exactly the same multiplication table. Hence, only permutations leaving vertex "1" fixed will be considered.

Figure 4a
Figure 4b
Comparison of Figures 4a and 4b above shows that reversing the handedness of all triads (i.e. reversing the directions of the arrows of all triangles) produces the same multiplication table as using the mirror-image triangles of Figure 1b; in either case the octonion representation:
(e1, e3, e2)
(e1, e5, e4)
(e1, e7, e6)
(e2, e4, e6)
(e2, e7, e5)
(e3, e7, e4)
(e3, e6, e5)
is the result, i.e. the XOR representation with signmask 77 (hexadecimal).

There are 6! = 720 permutations of the vertices 2-7 (leaving "1" fixed), but not all produce distinct representations; the same is true for the "mirror-image" representations (whether represented by reversing the directions of the triangles, or equivalently using the alternate triangles of Figure 2b).


Figure 5a
Figure 5b
Figures 5a and 5b above generate the same multiplication table as does Figure 3. Moreover, there is a simple relation among these 3 diagrams - Figure 5a is obtained from Figure 3 by doubling the angle of each vertex (so "2" is positioned at 2×2π/7, "6" at 2×4π/7, "3" at 2×6π/7, etc.); a second such angle doubling produces Figure 5b, and doubling angles a third time yields the original Figure 3 (because 23 = 1 mod 7). Since e1 occurs in 3 triads, there are 3 values of j such that ej can occupy the vertex one position clockwise from "1". The triangles have sides of length 1, 2, and 4 (in terms of clockwise angular distance); angle doubling for a triangle moves its vertices with new distances 2, 4, and 8 = 1 mod 7, preserving the shape and handedness of the triangle. Every triangle of the original diagram thus maps to a new triangle of the same shape, but with the numbering of its vertices cyclically rotated around the triangle - the triads remain the same though shifted in position, hence the same multiplication is still represented.

Dividing out this threefold degeneracy, permutation of the non-"1" vertex labels produces 6!/3 = 240 distinct multiplication tables for the octonions. A further distinct set of 240 is obtained by reversing the direction of all the triangles (or equivalently using the mirror-image triangles with non-reversed direction), giving a total of 480 distinct multiplication tables. This immediately implies that any diagram having uniform directedness of its triangles represents the true octonions, and conversely, every representation of the octonions can be represented by a diagram (actually 3) having triangles of uniform directedness.

Mixed Directedness

No diagram discussed so far mixes triangles of opposite directedness (though there may occur together in the same diagram triads of opposite handedness, since handedness depends on the numerical order of vertex labelling as well as direction of the triangle). It is now interesting to ask when a diagram of mixed directedness is equivalent to another diagram of uniform directedness.

Reversing the sign of a single imaginary unit results in a reversal of direction of the three triangles having that unit as a vertex, resulting in a new type of diagram having some triangles of each direction; however, a simple transformation yields an equivalent diagram (in the sense of giving the same multiplication table) in which all triangles have direction opposite to those of the original diagram (prior to reversing the sign of the unit). One such tranformation to a diagram with uniform has steps:
  1. reverse the direction of all triangles
  2. pick any one of the triangles containing the reversed unit
  3. identify the 4 points not on that triangle - 3 "grouped" on one side, 1 ("isolated") on the other
  4. exchange the indices of those 4 points, swapping the isolated point with the closest "grouped" point, and the 2 remaining "grouped" points with each other
Given a diagram with some uniform triangle directedness, an even number of sign reversals of unit elements will result in diagram representations having the same uniform triangle directedness, while an odd number of sign reversals of unit elements will result in diagram representations of opposite uniform directedness.

More generally, if some arbitrarily chosen subset of the triangles is reversed in directedness it will be possible to either find equivalent diagrams with uniformly directed triangles, or find equivalent diagrams with a single reversed triangle (which are not equivalent to any diagram with uniform triangle directedness). Diagrams with a single reversed triangle are in fact representations of the twisted octonions, the reversed triangle representing the distinguished triad, as below:
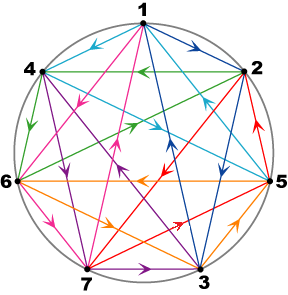
Triads:
(e1,e2,e3)
(e1,e4,e5)
(e1,e6,e7)
(e2,e4,e6)
(e2,e7,e5)
(e3,e4,e7)
(e3,e5,e6)

with distinguished triad (e1,e2,e3)